
Докажите, что закон равенства работ («золотое правило» механики) применим к гидравлической машине. Трение между поршнями и стенками сосудов не учитывайте.
Указание. Используйте для доказательства рисунок 144. Когда малый поршень под действием силы $F_{1}$ опускается вниз на расстояние $h_{1}$, он вытесняет некоторый объём жидкости. На столько же увеличивается объём жидкости под большим поршнем, который при этом поднимается на высоту $h_{2}$.
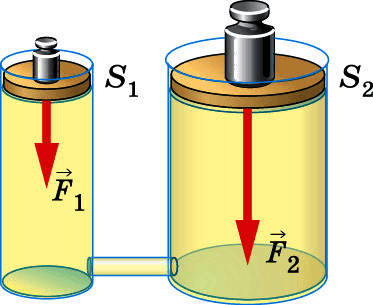
рис. 144. Принцип действия гидравлической машины

Устройство гидравлического пресса основано на законе Паскаля.
Два сообщающихся сосуда наполнены однородной жидкостью и закрыты двумя поршнями, площади которых $S_{1}$ и $S_{2}$ ($S_{2}>S_{1}$).
По закону Паскаля имеем равенство давлений в обоих цилиндрах: $p_{1}=p_{2}$.
Если на малый поршень действует сила $F_{1}$, то давление жидкости под
малым поршнем:
$p_{1} = \frac{F_{1}}{S_{1}}$
под большим:
$p_{2} = \frac{F_{2}}{S_{2}}$.
Отсюда
$\frac{F_{1}}{S_{1}} = \frac{F_{2}}{S_{2}}$;
$\frac{F_{2}}{F_{1}} = \frac{S_{2}}{S_{1}}$,
то есть при работе гидравлического пресса создается выигрыш в силе, равный отношению площади большего поршня к площади меньшего.
Малая сжимаемость жидкости обеспечивает практическое равенство объемов жидкости, переходящей из малого цилиндра в большой:
$V_{1} = V_{2}$, т.е.
$S_{1}h_{1} = S_{2}h_{2}$;
$\frac{h_{1}}{h_{2}} = \frac{S_{2}}{S_{1}}$.
Перемещение поршней в малом и большом цилиндрах обратно пропорционально площадям поршней.
$\frac{F_{2}}{F_{1}} = \frac{S_{2}}{S_{1}} = \frac{h_{1}}{h_{2}}$.
$F_{1}h_{1}=F_{2}h_{2}$, т.е.
$А_{1} = А_{2}$.
Равенство выражает "золотое правило" механики, применительно к гидравлическому прессу: "во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии".
Гидравлическая машина представляет собой механизм, работающий на основе закона Паскаля. Этот закон утверждает, что давление, производимое на жидкость в замкнутой системе, передается в любую точку этой жидкости без изменения. Рассмотрим взаимодействие двух поршней в гидравлической машине и докажем применимость закона равенства работ.
Когда малый поршень опускается вниз под действием силы $ F_1 $ на расстояние $ h_1 $, он вытесняет жидкость объёмом $ V_1 $, который можно выразить как:
$$
V_1 = S_1 \cdot h_1.
$$
Этот объём жидкости перемещается в область большого поршня, вызывая его подъём на высоту $ h_2 $. Под большим поршнем объём жидкости также равен:
$$
V_2 = S_2 \cdot h_2.
$$
Так как жидкость несжимаема и трение отсутствует, объёмы $ V_1 $ и $ V_2 $ равны:
$$
V_1 = V_2, \quad \text{то есть} \quad S_1 \cdot h_1 = S_2 \cdot h_2.
$$
Согласно закону Паскаля, давление в жидкости одинаково в любой точке системы. Давление под каждым поршнем можно выразить через силу, действующую на поршень, и площадь его поверхности:
$$
P = \frac{F_1}{S_1} = \frac{F_2}{S_2}.
$$
Из этого следует:
$$
F_1 \cdot S_2 = F_2 \cdot S_1.
$$
Работа, совершаемая силой $ F_1 $ на малом поршне при его перемещении на расстояние $ h_1 $, равна:
$$
A_1 = F_1 \cdot h_1.
$$
Работа, совершаемая жидкостью на большом поршне при его перемещении на расстояние $ h_2 $, равна:
$$
A_2 = F_2 \cdot h_2.
$$
Для гидравлической машины выполняется закон равенства работ:
$$
A_1 = A_2.
$$
Подставим выражения для $ h_1 $ и $ h_2 $ из равенства объёмов:
$$
S_1 \cdot h_1 = S_2 \cdot h_2 \quad \Rightarrow \quad h_2 = \frac{S_1 \cdot h_1}{S_2}.
$$
Также подставим соотношение сил из равенства давлений:
$$
\frac{F_1}{S_1} = \frac{F_2}{S_2} \quad \Rightarrow \quad F_2 = \frac{F_1 \cdot S_2}{S_1}.
$$
Теперь убедимся, что работы равны:
$$
A_1 = F_1 \cdot h_1, \quad A_2 = F_2 \cdot h_2.
$$
Подставим $ F_2 $ и $ h_2 $ в $ A_2 $:
$$
A_2 = \left(\frac{F_1 \cdot S_2}{S_1}\right) \cdot \left(\frac{S_1 \cdot h_1}{S_2}\right).
$$
Упростим выражение:
$$
A_2 = F_1 \cdot h_1 = A_1.
$$
Таким образом, работа, совершаемая на малом поршне, равна работе, совершаемой жидкостью на большом поршне. Это доказывает применимость закона равенства работ («золотого правила» механики) к гидравлической машине.
Пожауйста, оцените решение